C/ BAS DE LIGNE MATHEMATIQUE de "HOMO COSINUS"
(extrait
du topo général: "bas de ligne")
Seul un bas de ligne calculé mathématiquement voit son poids et sa raideur
(plus un brin est fin plus il est souple) décroître de façon constante de la
soie à la pointe, constance qui est le seul gage de l’équilibre indispensable
qui assurera un lancer « coulé » et un poser « léger »
Qu'il me soit tout d'abord permis de signaler que tout ce qui va suivre découle
de l'utilisation que j'avais faite il y a de nombreuses années d'un
article que j'avais ensuite perdu et dont j'avais oublié l'origine et l'auteur...ce
qui me désolait..jusqu'à ce que je reçoive dernièrement un message d'un lecteur
qui me permet enfin de "rendre à César ce qui appartient à César",
j'ai nommé JL Pelletier qui était donc l'auteur
de cet article à mon sens irremplaçable et que j'espère ne pas avoir dénaturé
ni trahi!!
Un autre article du même auteur donne des graphiques pour déterminer,
sans avoir besoin de faire les calculs,
la compositon d'un bas de ligne et tenant compte de sa "raideur"
qui varie en fonction du diamètre des différents brins,
*************************************
"J'ai retrouvé sur ton site tous les calculs des bas de ligne mathématiques
de J-L PELLETIER,vieux souvenirs de jeunesse.
J'ai eu le plaisir d'assister à quelques uns de ses cours sur la dynamique
des corps et des fluides. Et surtout, je n'ai pas manqué ceux où il
prenait la pêche à la mouche comme exemple d'application. Je me souviendrai
toujours de ses paroles "dans l'air, c'est de la cinétique, dans
l'eau , c'est de l'hydraulique".
Beaucoup
de personnes ignoraient, qu'en plus d'être ce Grand Bonhomme, excellent
pêcheur en sèche et en noyée, défenseur en son temps de l'écologie et
des rivières, il était d'abord et avant tout INGÉNIEUR en génie
mécanique et PROFESSEUR à l'École Nationale Supérieure des Arts
et Métiers de Paris. et je l’ai rencontré à plusieurs reprises.

Un
jour, en apprenant que je suivais mes cours de Construction au CNAM,
il m'a raconté très gentiment
qu'il
avait établi une méthode pour constituer "des bas de ligne mathématiques"
, il a sorti ses premiers tableaux de calculs et d'abaques dessinés
sur papier millimétré (Plus tard, il a simplifié son travail sous forme
des "tableaux de raideurs" pour que ce soit accessible à tout
un
chacun)
Il
m'a indiqué de même, qu'il avait l'intention d'expliquer les différentes actions
exercées sur la canne à mouche, suivies des réactions de la soie et du bas de
ligne lors des faux lancer, du shoot jusqu'au posé final ; Cela en application
de quelques un de ses cours sur la mécanique des corps(je te précise, ce n'est
pas du tout mon domaine) cinétique et hydraulique.
Il
m'a donc invité dans sa classe, mais je n'ai pu assister, tout timide, qu'à
un seul de ces cours; il m'y a donné gentiment et confiant, une copie de son
travail. Ces précieux documents que j'ai perdus ou égarés, il y a une dizaine
d'année.
Je
sais que parallèlement il souhaitait en faire la publication dans une revue
de pêche.
J'en
garde encore un souvenir ému . En tant que prof, il était si simple, si patient,
si précis et si clair que tu comprenais facilement sans être spécialiste. Cela
m'a fait faire d'ailleurs de très rapides progrès par la suite.
Voilà
Jean-Paul un peu de mes souvenirs et je me rends compte d'un coup, N
d D.. que ça doit faire trente ans!"
FRANCIS
*****************************************
En préambule, il est fondamental que
les "maso" qui décident de lire ce qui va suivre se munissent
d’un crayon et d’une feuille pour élaborer, chemin faisant, avec moi,
un bas de ligne « mathématique » car sans la « pratique »
qui, en famille, peut valoir le "scrabble" (!!?), la simple
lecture est carrément...."soporifique".....Je vous laisse
le temps de chercher de quoi écrire ou.....de sortir !!je vous
explique à quoi va servir le calcul :
Le bas de ligne "queue de rat" du commerce est le
seul vraiment régulièrement conique car usiné ainsi et son calibre
diminue en pente douce , sans transition: c’est une pente régulière,
l’idéal, sauf au niveau du prix et il n’est modifiable que par
ses extrémités
Le bas de ligne "à nœuds" que l’on se propose de fabriquer
(et que l’on trouve également dans le commerce) présente une dégressivité
en « escalier » par succession de segments bien distinct
de diamètre et de longueur décroissants.
Queue de rat ou à nœuds, un bas de ligne qui va de 40 à 14 sera d’autant
plus conique donc « rapide » (la mouche, arrivera d’autant
plus vite dans l’eau) qu’il est court,....pour la même impulsion de
lancer, dont on ne maîtrise pas parfaitement l’énergie transmise à l’extrémité
de la soie !
Mais avec le bas de ligne à nœuds, on peut, contrairement à la
queue de rat,(forcément dégressif) faire, entre le diamètredu
premier brin et celui de la pointe, « tout ce qu’on veut »,
alors il faut en profiter, puisqu'on on peut, en fonction du résultat
recherché, décider du nombre de brins et de leurs longueurs respectives
(décroissantes dans les dégressifs, croissantes pour les progressifs)
seul le calcul peut fixer leur
poids donc leur diamètre
pour que la perte d’énergie et de vitesse soit la plus
« régulière possible » et « complète » pour que
la mouche en fin de course,( ni trop tôt, ni trop tard) s’arrête
« en douceur » et tombe alors sur l’eau comme une feuille
morte: le poser a alors la précision et la légèreté souhaitées

alors que…. si la pointe est trop courte, la mouche
« matraque » l’eau,.... trop longue , la précision ne sera
plus au rendez-vous !!
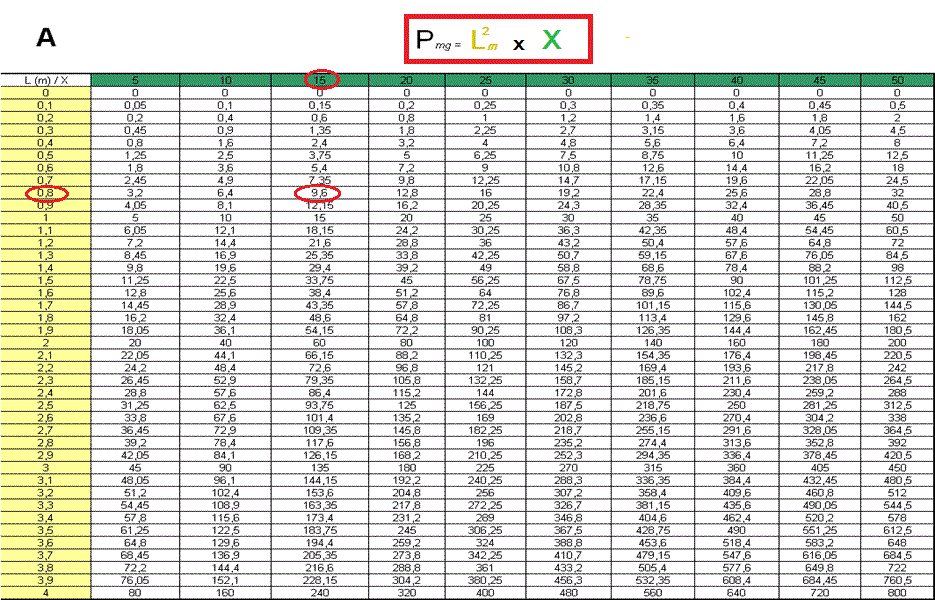
La fonction P mg = L2 m x X
de JL Pelletier donne une variation constante du poids en
milligrammes du bas de ligne en fonction du carré de sa longueur
en mètres , le coefficient X variable permet tous les choix
de poids du bas de ligne pour une longueur donnée.(4m dans tous les
exemples qui suivent) , c'est donc un "coefficient de puissance"(laquelle
dépend aussi de la conicité)
1/Les données indispensables

-
le tableau
A donne à partir de l’équation, les poids calculés de
différents bas de ligne mathématiques en fonction de
leur longueur et de différentes valeurs du coefficient
X,
étant admis que la densité
du fil de nylon "standard" = 1,14 arrondie à 1
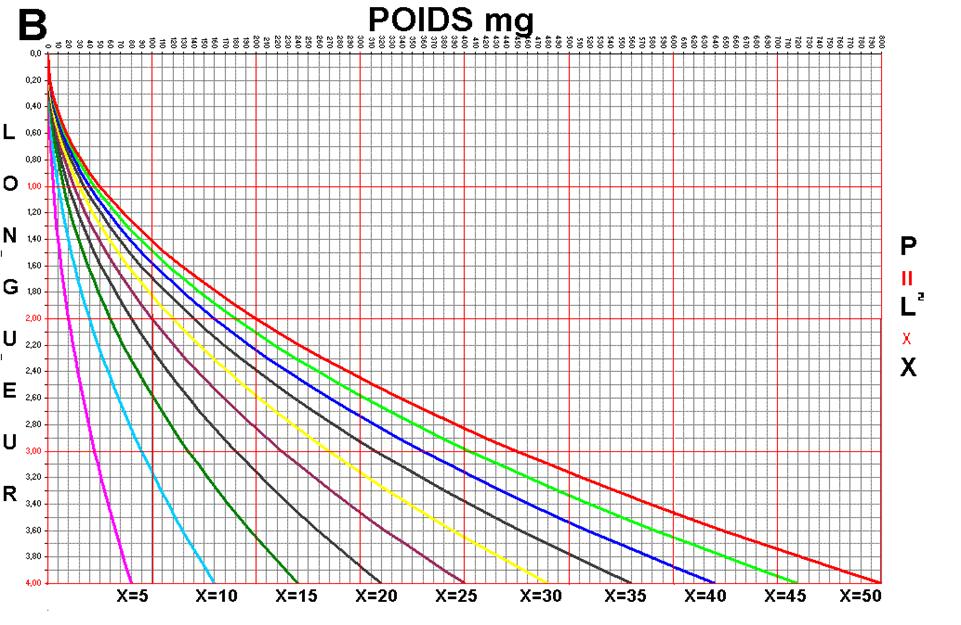
- les courbes
B sont les représentations graphiques de ces mêmes bas
de ligne calculés à partir de l’équation
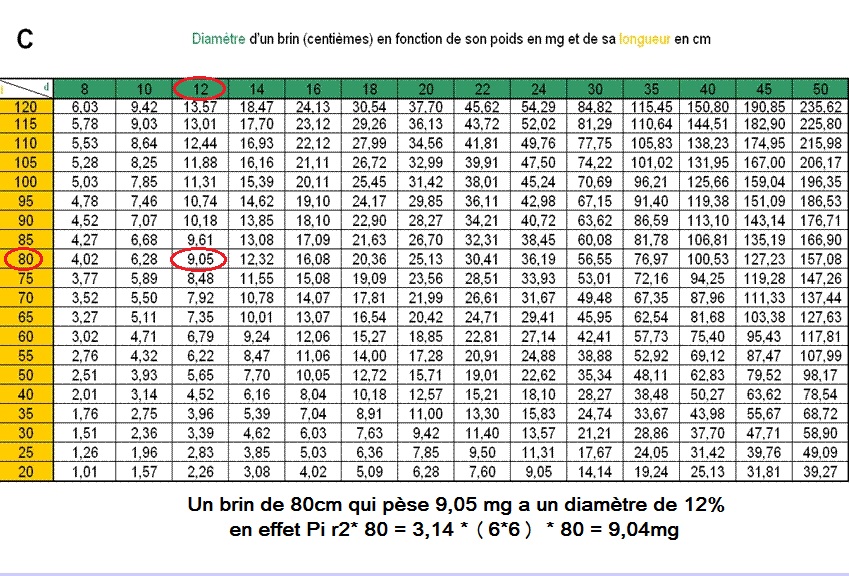
- Le tableau
C n’a rien à voir avec l’équation mais correspond aux caractéristiques
de fabrication du nylon ce qui permet à partir du poids (mg) et de
la longueur (en cm colonne de gauche) d’un brin d’en déduire son diamètre
(ligne du haut) toujours en attribuant au
fil une densité de 1 (contre 1,14 réelle pour le nylon)
pour simplifier les calculs
2/Utilisation des données pour monter un bas de ligne équilibré
mathématiquement
En premier lieu prenons pour exemple un bas de ligne
standard de 4m de puissance moyenne de 39% à 14% en 6 brins élaboré
par le tableau excell, lui même conçu en fonction de la
formule P mg = L2 m x X, afin de le comparer "in fine"à
celui que l'on va essayer de monter "identique" manuellement!
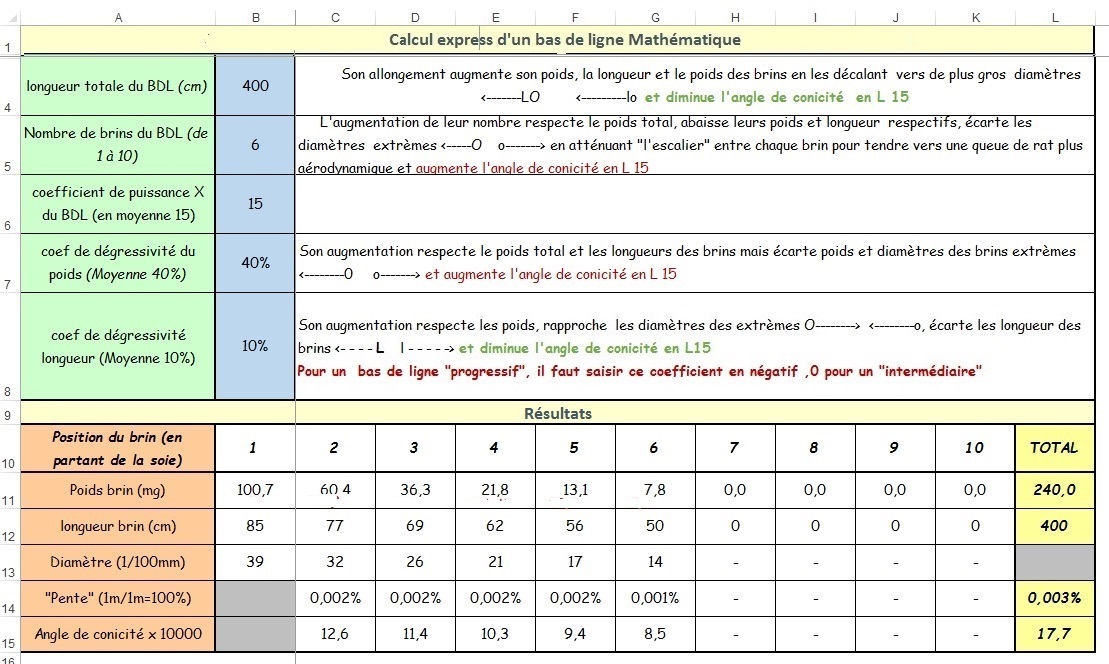
Certains des résultats ci dessus(longueurs,
coeff de puissance , dimensions du premier brin et de la pointe)vont
en effet servir d' éléments de départ indispensables
à cette élaboration, et ainsi permettront de faire la
comparaison entre les deux démarches!

a)Choix des extrémités : un simple coup
d’œil (sur les courbes B et les tableaux A et C) va permettre de définir
d’avance le diamètre des extrémités du bas de ligne, pointe et premier
brin après la soie
On choisit en premier le diamètre et la longueur
de la pointe(ici ceux donnés par le tableau
excell) dont le poids va imposer le coefficient X qui multiplié
par le carré de la longueur que l’on choisit ensuite déterminera le
poids total du bas de ligne
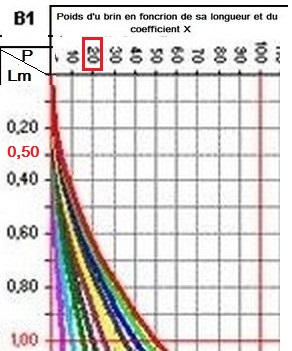
la pointe :
si l’on s’en tient à une longueur de 50 centimètres
nécessaire et suffisante pour un posé correct, et à un diamètre de 14/100,
(cases 6) on constate sur
le tableau C que cette pointe pèsera 7,8mg et sur les
courbes B, que ce n’est qu'au dessous coefficient de 20
que le poids de ces 50 centimètres reste = ou
inférieur à 10mg, ! !Il faudra donc bien se
tenir en deçà du coefficient 20 pour que l’équilibre du bas de ligne
se satisfasse d’une pointe égale (ou inférieure) à 14 centièmes, car
au dessus , l’équilibre du bas de ligne nécessitera des poids supérieurs
de la pointe et des brins
(A ce sujet, il est important de savoir que quelle que soit la "formule"
définitive du bas de ligne , il y a une règle à respecter
pour les brins de "petit diamètre" inférieur à
18%:
En effet, si l'on peut dans les gros diamètres passer,
sans compromettre la solidité, par de grands écarts de 5%, voire
plus (de 40% à 35%, voire même 30%), il faut parait-il à
partir du 18%, ne plus tolérer que des écarts de 2%........et
descendre alors en passant par le 16%, le14%, le12%.........et non 18%-14% par
exemple sous peine de fragiliser le 14%!
Ceci peut amener à "adapter" en pratique
les diamètres théoriques issus des calculs!
(à ceci près
que les diamètres annoncés ne sont pas toujours le reflet
de la réalité!!)
le premier brin :
sur ce bas de ligne de 4 mètres, choisissons un premier brin, qui fait
suite à la soie, d'une longueur de 0,85 mètre
issue du tableau excell ; ce premier brin, qui devra
avoir un « calibre » adapté à la pointe de la soie, notamment
en raison de la « raideur » du nylon, bien supérieure à celle
de la pointe de la soie malgré la différence de diamètre (ce qui pour
certains demanderait un calibre bien inférieur aux 40, 45, voire 50%
préconisés classiquement par la plupart) représentera en fait les derniers
85 cm(case1) sur les 4 mètres de
ce bas de ligne mesuré à partir de la pointe. Si le coefficient
de X est de 15 , on constate sur la courbe B correspondante
que ce brin fait passer le poids du bas de ligne de 139,4 mg pour 3,14m
à 240 mg pour 4mètres et qu’il pèsera donc 100,74 mg.
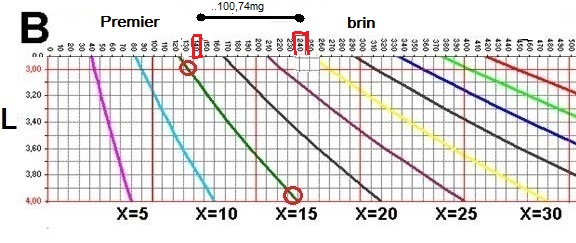
Si l’on se reporte au tableau C, on constatera qu’un brin de
85 cm qui pèse 100,7mg correspond à une diamètre de 40 centième qui
sera donc le diamètre imposé mathématiquement à ce premier brin dont
le poids réel est le plus proche du chiffre théorique calculéde 106,81mg
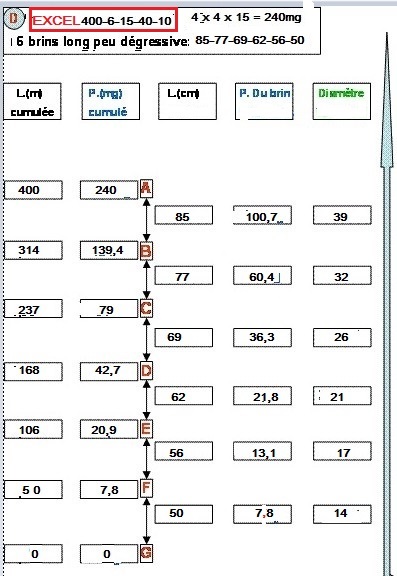
b)Le montage proprement dit du corps du bas de ligne correspondant
à celui proposé par le tableau excell pour les données
400-6-15-40-10
- Envisageons donc ce bas de ligne de 4 mètres terminé
par une pointe de 50cm en 14 centièmes pour 7,8mg pour
un coefficient de puissance 15
4 m x 4m x 15
= 240 mg
- Suivant cette formule excell a réalisé
un bas de ligne de : 6 brins de 0,85-0,77-0,69-0,62-0,56 et 0,50cm
pour la pointe, longueurs que l'on reprend ici toujours à des
fins de comparaison et que l'on présente sur le tableau ci
dessous
-
- Reste à calculer r "manuellement" le
diamètre de chacun de ces 6 brins à
partir de leur longueur connue et de leur poids respectif (toutes
dimensions données par excell mais que l'on veut ignorer)
qu'il faut donc ici calculer en premier
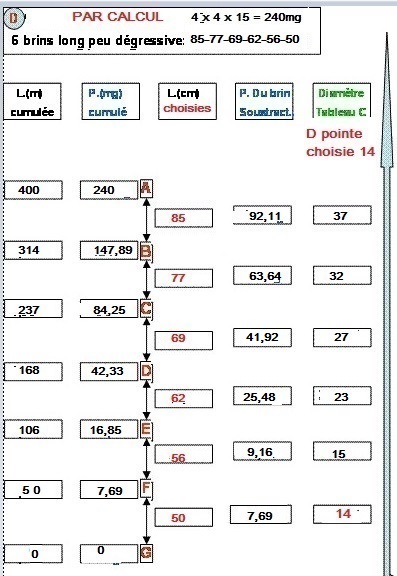
On trace le schéma D
de ce bas de ligne A – G de 240 mg pour 4 mètres en 6 brins de longueurs
définies ci dessus, le premier faisant suite à la soie, le 6ème
représentant la pointe.
Le poids en mg d'un brin de densité =1 est celui
du volume en mm3 du cylindre qu'il représente calculé
selon la formule

La pointe (6) F-G=………………………………7,69mg pour 50cm de 14/100
On calcule à l’aide de l’équation, les poids cumulés des segments
de brins successifs ( tableau A)
E
– G = 1,06m x 1,06m x 15 =………….
16,85mg
D – G = 1,68m x 1,68m x 15=……………… 42,33
mg,
C – G = 2,37m x 2,37m x 15 =……………… 84,25mg,
B – G = 3,14m x 3,14m x 15 =………………147,89 mg, et enfin
A – G, le bas de ligne complet =4 x 4x 15= 240 mg.
On calcule le poids de chaque brin par une simple soustraction
Pour le brin N°…. 5, E – F, le poids est de E – G moins F – G =9,16mg
pour… 56 cm
........................... 4, D – E, .....................
D – G moins E – G = 25,48 mg pour....62 cm
.......................... 3, C – D,......................
C – G moins D – G = 41;92 mg pour……69 cm
............................ 2, B – C,...................... B
– G moins C – G = 63,64 mg pour .......77 cm
.............................1, A – B,...................... A – G
moins B – G = 92,11mg pour....... 85 cm
A
- G, le bas de ligne complet par addition = 240mg
On se réfère au tableau C avec la longueur et le poids
de chaque brin pour obtenir, au besoin en extrapolant, les diamètres
correspondants
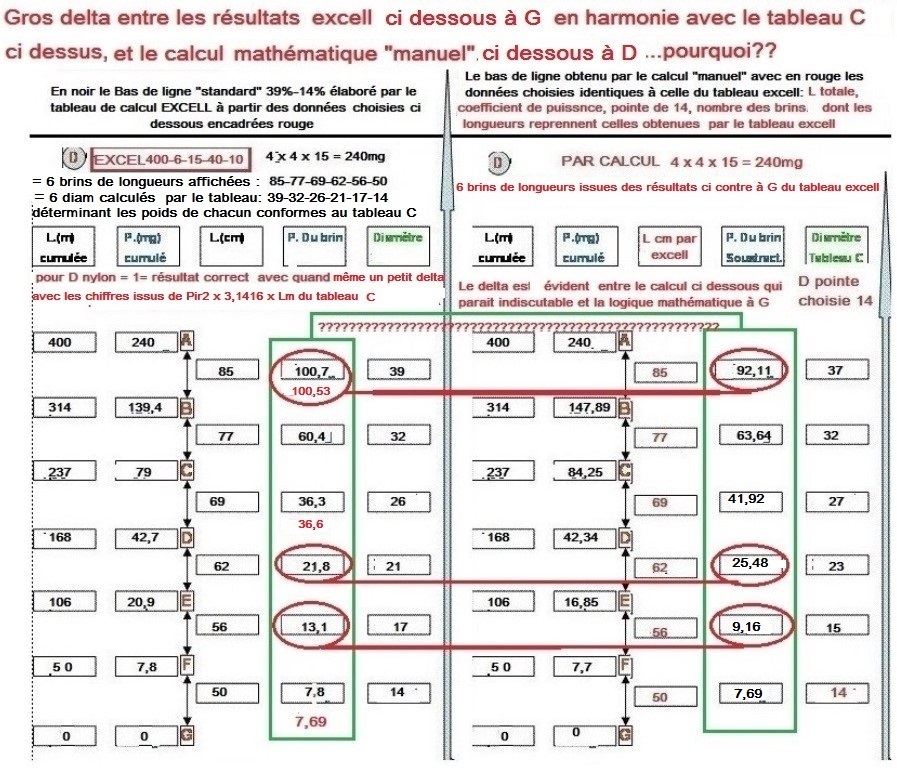
On constate alors
oh, surprise...
que par le calcul manue l on arrive par rapport aux
résultats du tableau excell, et pour des brins d'une même
longueur, à des diamètres un peu différents en
rapport avec des poids différents
mystère de l'informatique??
*****************************
Bien...si vous désirez désormais
retourner au XXIème siècle, c'est
par là...!
******************


|